数据结构与算法之冒泡排序

概念

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。

原理

比较两个相邻的元素，将值大的元素交换到右边。如果遇到相等的值不进行交换，那这种排序方式是稳定的排序方式。

思路

依次比较相邻的两个数，将比较小的数放在前面，比较大的数放在后面

1) 比较第1和第2个数，将小数放在前面，将大数放在后面。
2) 比较第2和第3个数，将小数放在前面，将大数放在后面。

...依此类推

3) 当比较到第一轮最后两个数时候，将小数放在前面，将大数放在后面；其中最后一个数肯定是整个数组中的最大数，所以在接下来的轮次中是不需要参与比较的。
4) 在上面一轮比较完成后，需要重复如上步骤，每一轮比较次数依次减少，并且每一轮过后都会有一个不需要参与下轮比较的值，直至全部排序完成。

图解冒泡排序

需要参与冒泡排序的数组: [24, 0, 300, 69, 80, 4, 293, 57, 13]

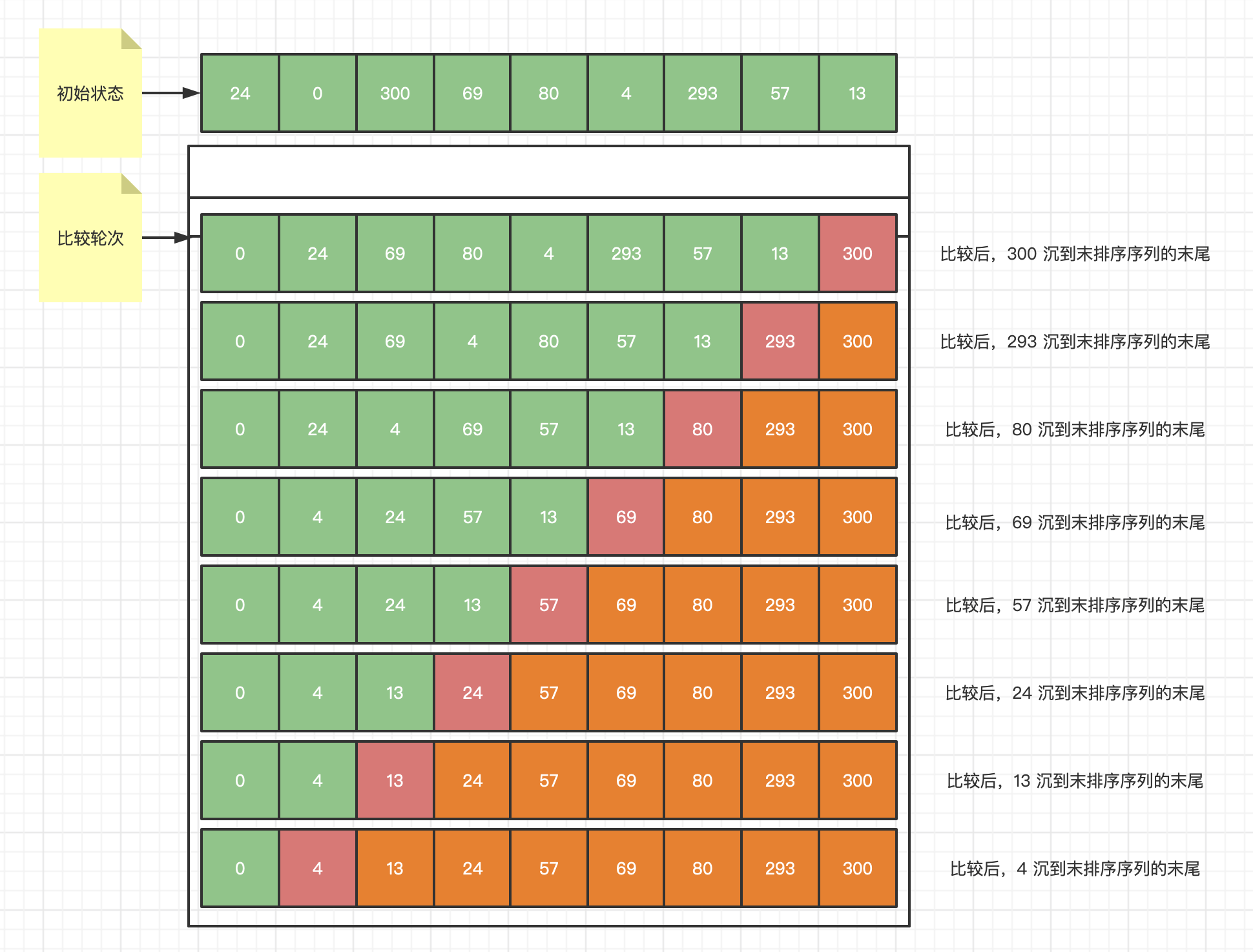
算法分析可以看到:

• 逻辑处理: N个数字要排序完成，总共进行 N-1 轮次排序，每一次的排序次数为(N-i)次。所以可以用双重循环语句，外层控制循环总轮次，内层控制每一轮的循环次数。
• 规则原理: 每进行一轮次排序，就会少比较一次，因为每进行一轮排序都会找出一个较大值。如上例: 第一轮比较之后，排在最后的一个数一定是最大的一个数，第二趟排序的时候，只需要比较除了最后一个数以外的其他的数，同样也能找出一个最大的数排在参与第二轮比较的数后面，第三轮比较的时候，只需要比较除了最后两个数以外的其他的数，以此类推…… 也就是说，每进行一轮比较，每一轮少比较一次，一定程度上减少了算法的量。
• 时间复杂度:
  (1) 如果我们的数据正序，只需要走一轮即可完成排序。所需的比较次数C和记录移动次数M均达到最小值，即：Cmin=n-1; Mmin=0; 所以，冒泡排序最好的时间复杂度为O(n)。
  (2) 如果很不幸我们的数据是反序的，则需要进行n-1轮次排序。每轮次排序要进行n-i次比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值。
  冒泡排序总的平均时间复杂度为：O(n^2) [n的平方] , 时间复杂度和数据状况无关。

接下来用 Go 实现冒泡排序算法代码

package main

import "fmt"

/******* 冒泡排序法 *******/

func main()  {
    var arr = [9]int{24, 0, 300, 69, 80, 4, 293, 57, 13}

    for j := 0; j < len(arr) - 1; j++ {
        var oldArr = arr
        var nextTotalLen = len(arr) - j - 1
        for i := 0; i < len(arr); i++ {
            if i < nextTotalLen {
                var nextKey = i + 1
                if arr[i] > arr[nextKey] {
                    // 前面值大于后面值时, 位置置换
                    var nextVal = arr[i]
                    arr[i] = arr[nextKey]
                    arr[nextKey] = nextVal
                }
            }
        }

        // 值完全相同则不需要继续循环下去了
        if oldArr == arr {
            break
        }
    }

    fmt.Println(arr)    
    /**
        输出: [0 4 13 24 57 69 80 293 300]
    */
}